When you were little did you ever jump rope, or if you were a little boy like me did you at least watch the little girls as they jumped rope? If you did then you are familiar with the shape that the rope takes as it’s being twirled around. You remember how it sort of has a hill shape when the rope is above the jumper’s head and the exact opposite valley shape when it’s coming down and she has to jump over it.

Later on, in high school, you may have learned in your math class that the shape the rope takes is that of the trigonometric function known as the Sine of an angle, Sin (θ). Or more properly a jump rope is half of a sine wave, the positive half on the up stroke and the negative half on the down.
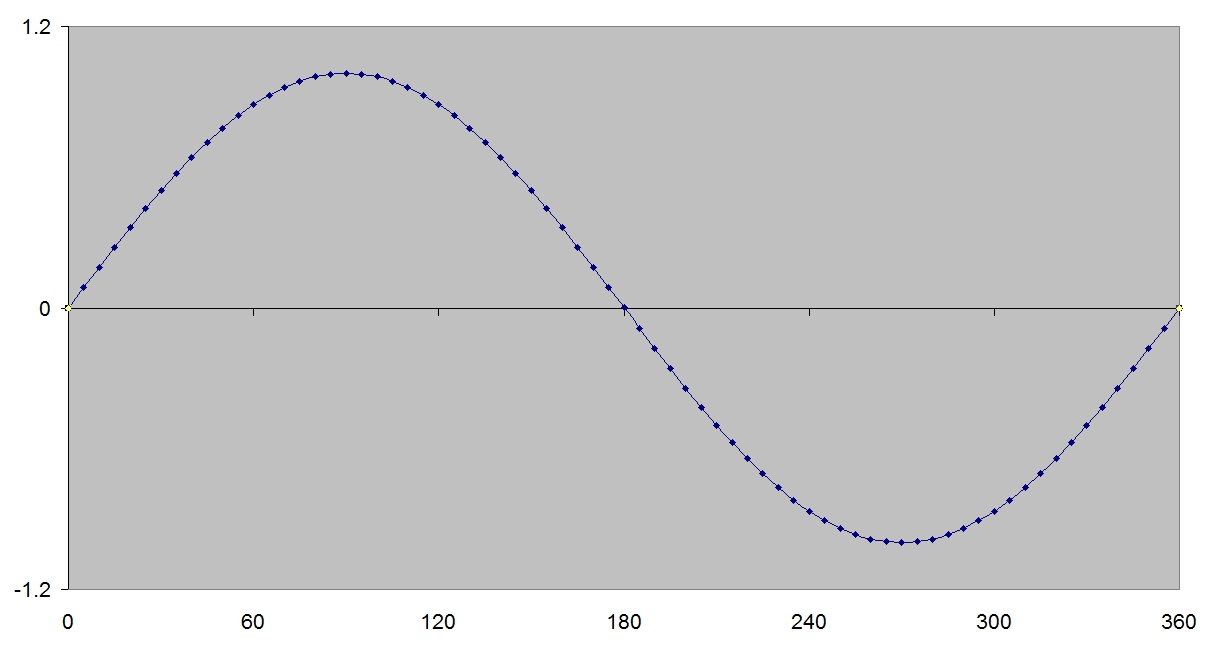
Now that half a wave phenomenon is an important point, because if you take a jump rope and twirl it really fast you can actually get a shape that is two-half waves, one up one down which of course makes a full sine wave. Even faster and you get three halves or 1½ waves, and so on. When I taught freshman physics I would always take a jump rope to class when we started to study waves and by tying one end to a door knob and twirling the other as fast as I could I usually managed to get six half or three full waves.

No matter how hard you try however, you will never get 2/3 of a wave, or 1¼ waves or something like π waves. Only integer multiples of ½ of a wave are allowed, ½, 1, 1½, 2, 2½, 3 and so on. In physics these special values have been given the name Eigenvalues, which is German for characteristic values.
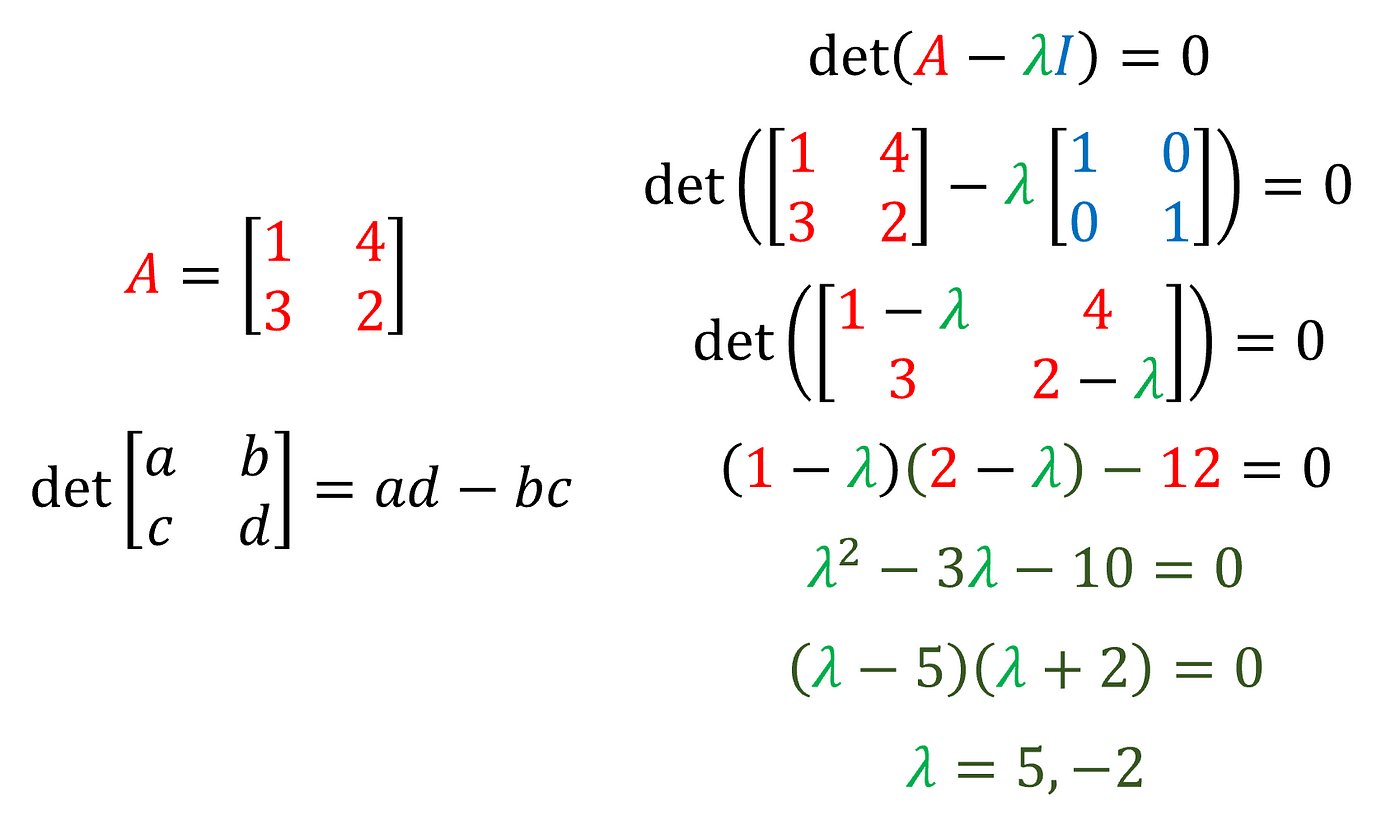
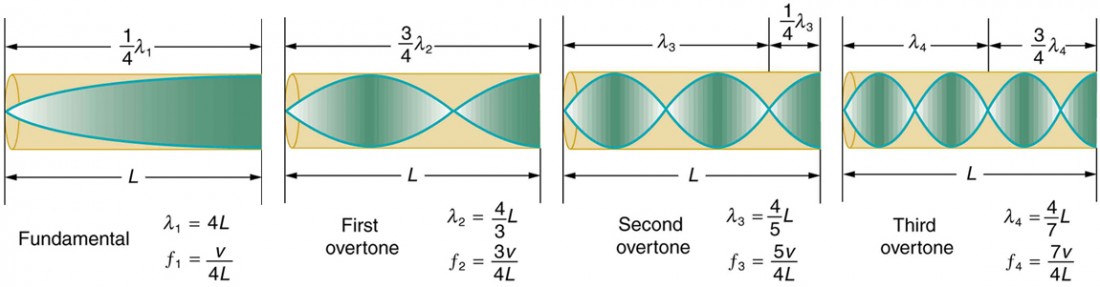
Eigenvalues are a fundamental attribute of every musical instrument. For example when you pluck a guitar string you get a shape very much like a jump rope, a half wave vibrating up and down and the speed of that vibration is the frequency of the sound that you hear. In a similar way the eigenvalue of an single organ pipe can be calculated so that it will sound the right note.
If you want to try a simple experiment take a 16oz. bottle of soda and drink about half of it. Then, holding the bottle upright so the soda doesn’t spill out, blow across the opening at the top, what you’ll hear is a fairly high pitched note. Now drink about another quarter of the soda so you still have about a quarter of it left and repeat blowing across the opening. Notice how the note is different; it’s a lower note. Finally finish your drink and repeat blowing across the opening; the note will sound even lower, deeper.

It’s the size of the air chamber in the bottle, along with its shape, that determines the frequency or the note you hear. The larger the chamber the larger the fundamental eigenvalue and therefore the lower the note.

All musical instruments make use of this eigenvalue phenomenon and being able to calculate the eigenvalues of an instrument is important in being able to design one. Now the examples I’ve talked about so far, the jump rope, guitar string, organ pipe and even the soda bottle are all basically one dimensional systems. Even for the soda bottle it’s the longest dimension that primarily determines the fundamental frequency.

There are two dimensional instruments as well, the best known of which are drums, that flat sheet of animal skin stretched across the round drum base is what vibrates to create a sound. Now a two dimensional problem like the disk of a drum is quite a bit more difficult to calculate than the one dimensional one, orders of magnitude more difficult in fact. You can actually get a two dimensional disk to vibrate in different ways by striking it in different places. Striking a drum head in the center causes it to vibrate something like a jump rope, if you looked at a cross section at least. Striking the drum head off center however can cause one side to go down while the other side goes up in a fashion unlike any one dimensional wave.

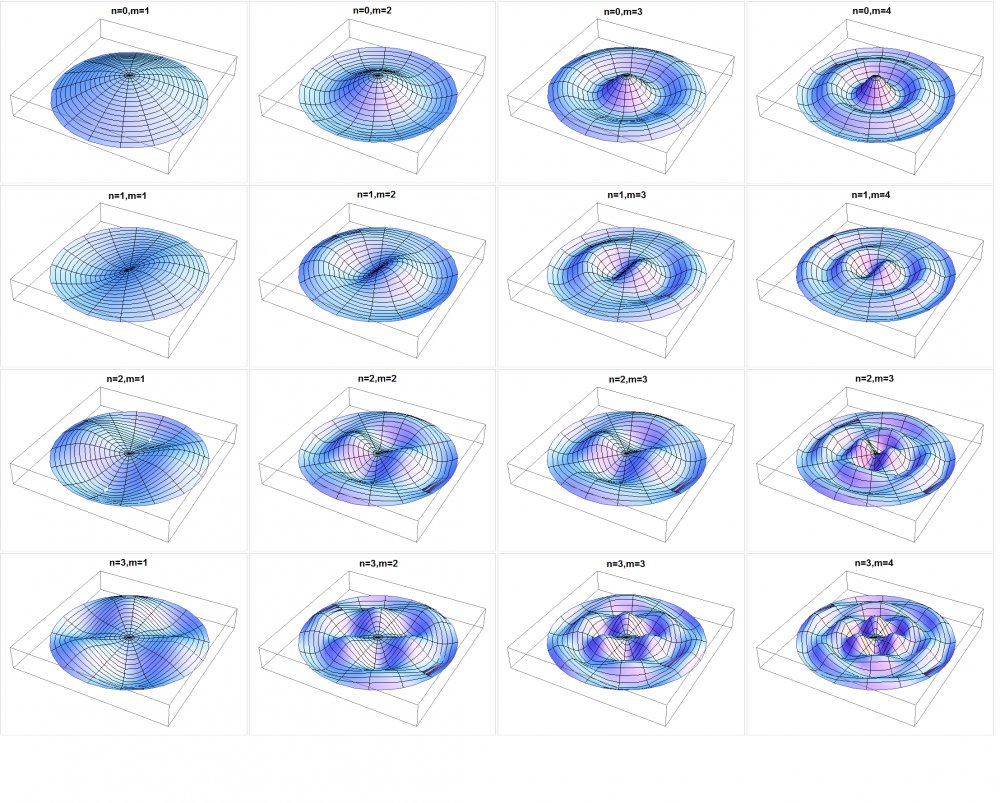
Back in 1954 a mathematician named George Pólya stated a conjecture where you could calculate the shape of a two dimensional surface from the frequency of the sounds it gave off. Pólya succeeded himself in proving his conjecture for a two dimensional surface that is made up of shapes that tile together, see my post of 22 April 2023 for more information on geometries that tile. Round disks, like a drum head, however do not tile and Pólya never managed to prove his idea for disks.

Now an international team of mathematicians, Nikolay Filonov from Steklov Institute of Mathematics in St. Petersburg Russia, Michael Levitin of the University of Reading in the UK, Losif Polterovich from the University of Montreal in Canada and David Sher of DuPaul University in the US, have succeeded in proving Pólya’s conjecture for disks. Their proof has been published in the journal Inventiones Mathematicae and while that proof may be an abstract piece of mathematical analysis it could also lead to practical applications in many fields, not just music.

Eigenvalues are a factor wherever waves occur, acoustics, hydrodynamics, electronics and perhaps most famously in quantum mechanics. So any advance in our understanding of eigenvalues is a step forward in our understanding of the world around us.
