Just a couple of weeks ago, 14 October, I published a post discussing the winners of the 2020 Nobel prizes in the sciences. While I covered the recipients of the physiology, physics and chemistry awards I purposefully skipped the winners of the Nobel for economics.
You see Paul Milgrom and Robert Wilson, both of Stanford University in California, were recognized by the Nobel committee for their work in the branch of mathematics known as Game Theory and I was planning to write a post about game theory. I decided therefore to wait and include Professors Milgrom and Wilson in this post.

Now we all have played games in our lives, and we know that most of those games involve some degree of chance or luck, various outcomes each have there own probability of occurring. But game theory is not probability theory, although there is certainly some overlap.

As an example, in a game of poker probability theory can tell you exactly what your chances are of filling an inside straight. Game theory on the other hand will help you decide whether or not trying to fill an inside straight is a good strategy to win the game. In other words game theory is about making decisions. Not just in contests but also in everyday life by treating our interactions with each other as games that we are trying to win. The two main assumptions in game theory are that the decision makers, unsurprising known as players, are rational, that they want to maximize the benefit to them, and that they understand the game they are playing enough to make competent decisions.

One of the best-known and most often discussed problems in game theory is known as The Prisoner’s Dilemma. This game is often described as having two men who have committed a crime of some sort, been captured by the police and separated. The separation is important in order to keep they two players from acting in concert.
The police have some evidence against the two prisoners but not a lot so they would like to get one of the crooks to confess and rat on his buddy. So the police separately offer each crook a deal for a light sentence if he’ll cooperate. The other crook would then get a full sentence.
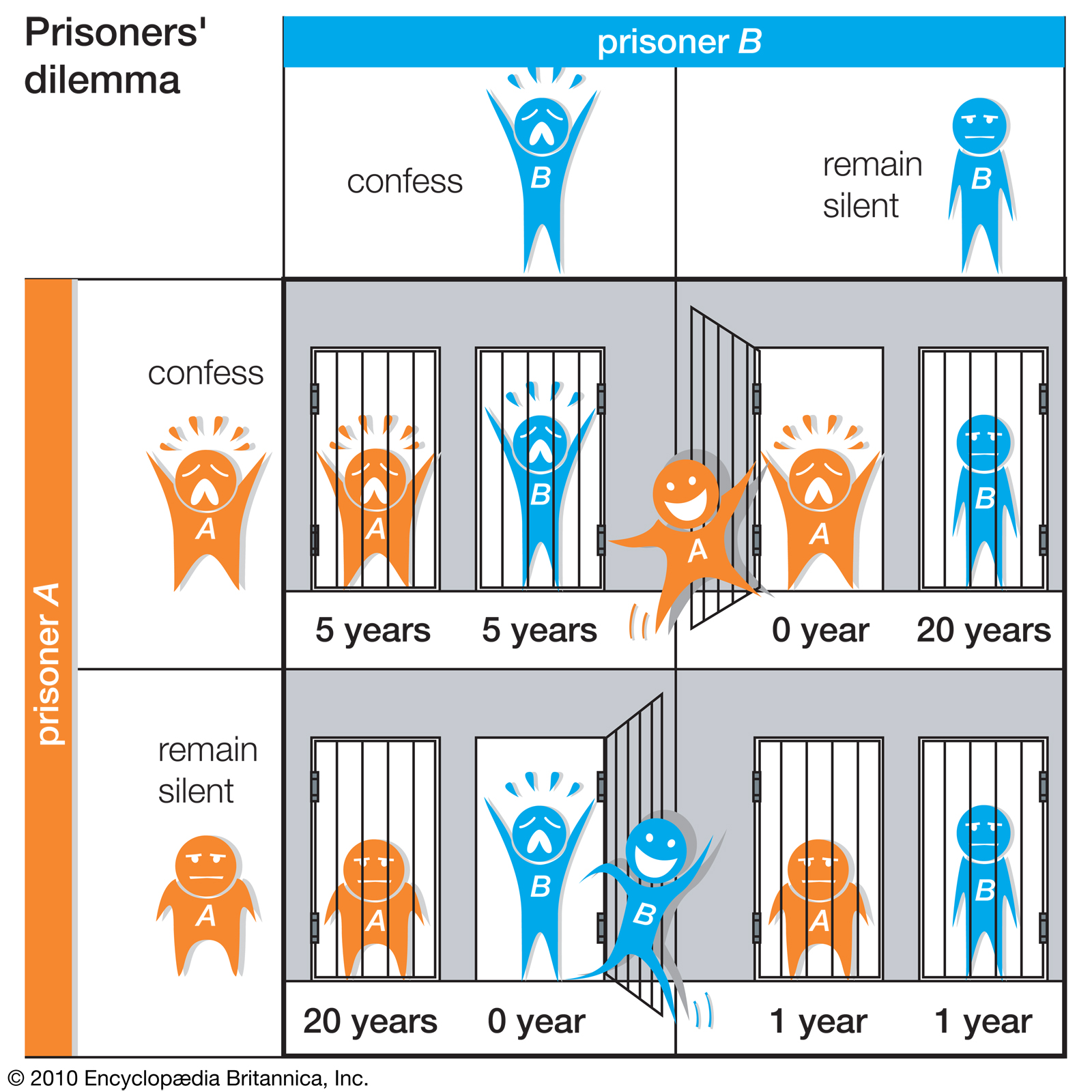
If both criminals refuse to cooperate there’s a fair chance that they could both go free but there’s a 100% chance of a light sentence for betraying the other guy. And remember the prisoners are separated so they have no idea what their cohort will do. Trust is a hard thing to do if you’re afraid that the other guy could be selling you out!
This kind of situation actually crops up all the time in real life, basically anytime two people have to trust each other in order to maximize their shared gain. Whether it be some form of commerce between two individuals or anything up to two nations forming an alliance in war the prisoner’s dilemma plays a large part and history has shown that whenever things start to go wrong the most often chosen solution is to stab the other guy in the back! In fact the prisoner’s dilemma has been used to explain why so many different kinds of animal become instantly hostile when confronted by another member of their species. Yes game theory has its uses in evolutional theory too.

At least betrayal is the best solution to a single prisoner’s dilemma game. You see game theory also has to consider the possibility of multiple prisoner’s dilemma games between the same two players, such as in international trade which can go on for centuries. In such circumstances it can be shown that after just a few games the benefits of trust quickly outweigh the risk.

Almost any sort of human interaction can be modeled as a game and therefore subject to analysis by game theory. All that is required is that the individuals involved are making rational decisions based on their knowledge of the situation.
One of the most important concepts in game theory is known as a Nash Equilibrium, named for Nobel Prize winner John Nash who was the subject of the 2001 movie ‘A Beautiful Mind’. In the prisoner’s dilemma game discussed above the Nash equilibrium is for both of the crooks to confess.

Another easy example is sometimes known as ‘The Battle of the Sexes’ and involves a couple who are going out on a date. Now say the man wants to go to a sporting event while the woman wants to go to a concert, but since this is a date the important thing is that they go together. The Nash equilibrium in the case is that they both either attend the sporting event or the concert. As you can see game theory is really about using logic rather than branches of mathematics like calculus or trigonometry.

Now game theory is not without its problems. You’ll recall I said above one of the main assumptions is that the players are rational. Well experimental psychologists have long criticized that assumption. Another common criticism is that game theory fails to take in account the fact that some players are better at the game than others, that some of us are talented.

Nevertheless game theory has become an important tool in evolutionary studies, political science and especially economics. Which brings us back to professors Milgrom and Wilson whose work in game theory involved developing methods for analyzing auctions. In particular they developed formats for certain auctions where the interest of the auctioneer is to benefit everybody, i.e. society, rather than just maximizing their own profit.

The auction formats developed by Milgrom and Wilson were put into practice by the US government in 1994 when the Federal Communications Commission (FCC) auctioned off certain radio frequencies for use in the first cell phones! Unlike much of game theory the work of Milgrom and Wilson has already found considerable practical applications.
Still game theory is one of the newest branches of mathematics, and is rapidly growing. I expect that more Nobel prizes are in the future for game theory.
