Day: April 14, 2021

Mathematicians have been in love with Prime Numbers for almost three thousand years. Today they are even defining new classes of primes just to have the fun of studying them.

 We all remember Prime Numbers from our high school math classes. You know, those numbers that can only be evenly divided by themselves and one. For example since the number six can be divided into two times three (6=2×3) it is not a prime number. Seven on the other hand cannot be divided by any number except itself and one so seven is a prime number.

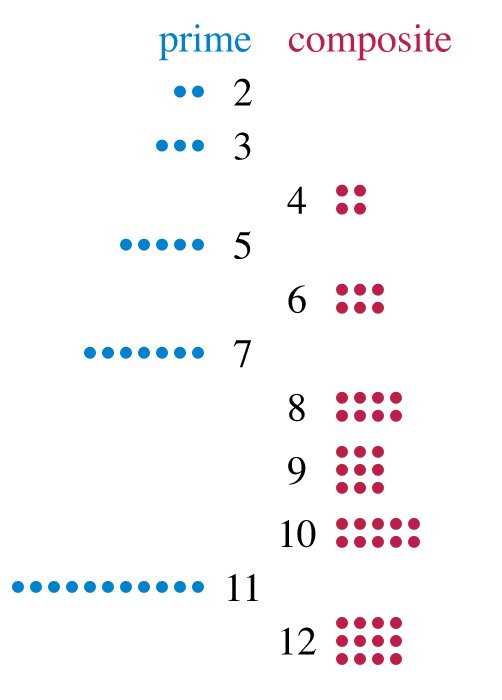
The first 12 whole numbers arranged as prime, left side, or composite, right side. While composite numbers can be arranged as rectangles prime numbers can never be arranged as anything but a straight line! (Credit: Wikipedia)

All non-prime numbers are called composite numbers because they can be broken down into their prime factors. For example again 6 can be broken down into 2×3 while 8 can be broken down into 2x2x2 and 36 is 2x2x3x3.

The number two is the only even prime number since by definition an even number is one that can be divided by two! Also while there are a lot of primes down close to zero; one, two, three, five, seven and eleven for example are all primes, as the numbers get larger the distance between primes gets bigger. For example there are five prime numbers between 1 and 10: 1, 2, 3, 5, and 7. However there are only three prime numbers between 80 and 100: 83, 89 and 97.

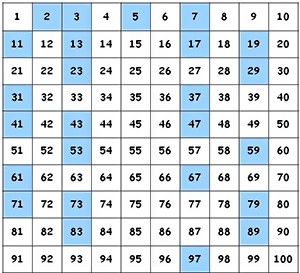
One age old technique for finding the prime numbers less than, say 100 is to eliminate the multiples of 2, then eliminate multiples of 3, you’ve already eliminated 4 so move on to multiples of five. Keep doing this for all numbers that you haven’t eliminated and at the end you’re left with only prime numbers. This technique is called the sieve. (Credit: Computer Hope)

Nevertheless it is easy to prove that there are an infinite number of primes, so easy in fact that I’m going to do it right now:

We start by assuming the opposite, that there are only a finite number of primes, N, and prove that assumption doesn’t work. So, if there are a finite number of primes we can designate them as p1, p2, p3…all the way out to pN the last prime. If we have all of the prime numbers we can then multiply all of them to get:

MP=(p1xp2xp3x…pN)

If we now add one we get:

MP+1=(p1xp2xp3x…pN)+1

If we try to divide this number by any of our primes, say p15 we will get a remainder of 1/p15. MP+1 is not evenly divisible by any of our primes! That is only possible if it is itself a prime or if it is composed of primes not in the set we said was complete. Either of these two possibilities breaks our assumption so we have proven that it is not possible even in theory to collect a set of all prime numbers, they must be infinite in number! This proof that there are an infinite number of primes goes all the way back to the Greek mathematician Euclid, often called the father of geometry.

Euclid’s ‘Elements’ are still the basis for the mathematics of geometry and are one of the greatest achievements in the history of mankind. (Credit: Biography Online)

Mathematicians have tried for centuries to see if they could derive a formula that will always give them prime numbers. Many such equations work for a while but to date every one that’s been tried has failed eventually. The one below works for integers up to 79 but fails at 80.

N2-79+1601= Prime Number for N a positive integer < 80.

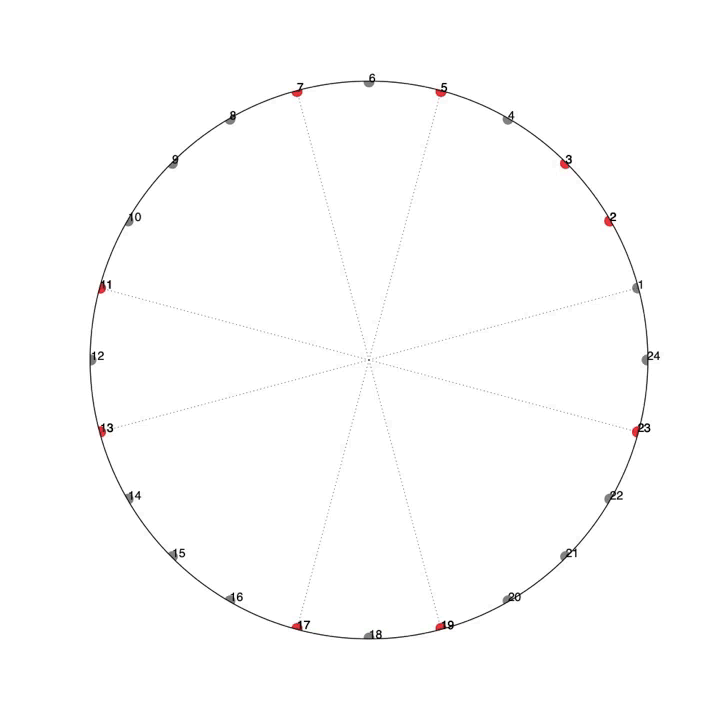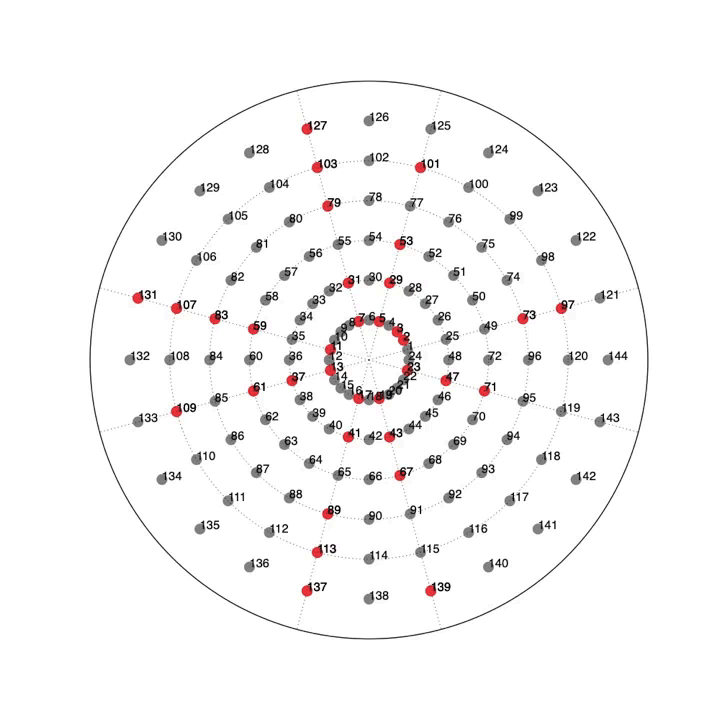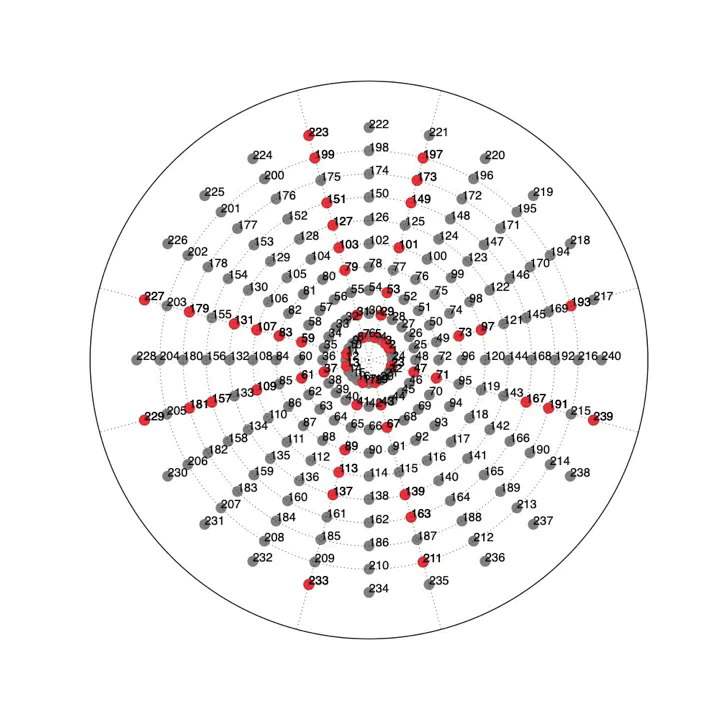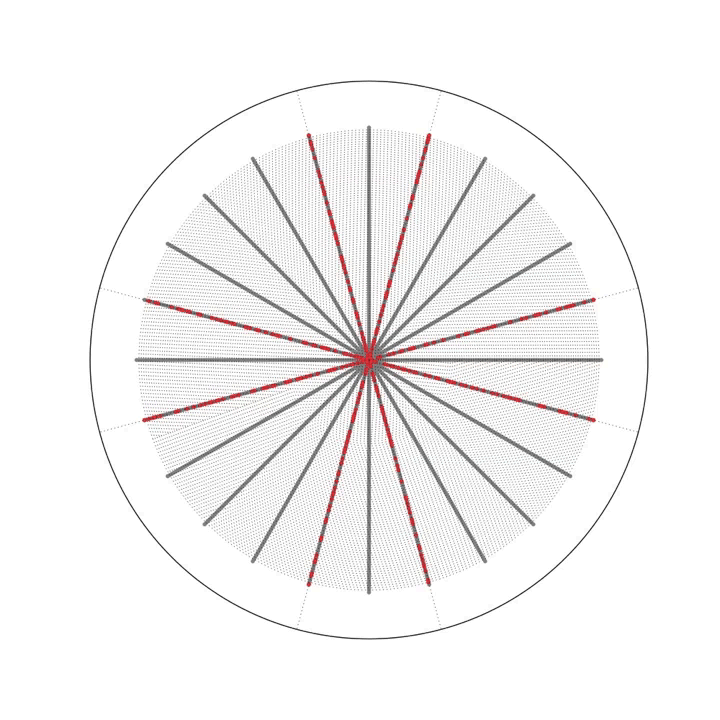
Another interesting, possible technique for finding primes is called the Prime Numbers Cross discovered by German chemist Peter Plichta where when numbers are arranged in progressive circles of 24 numbers per circle the primes occur on 8 spokes radiating out from the center, but not all numbers on those spokes are prime. (Credit: Beyond the Standard Model Pub)

Another interest thing about primes is that they have a habit of coming in pairs, two odd numbers in a row who both turn out to be prime. There are six such pairs less than 100: 11 and 13, 17 and 19, 29 and 31, 41 and 43, 59 and 61 and 71 and 73. The number of these pairs has recently been proven to be infinite as well but I won’t go into the proof both because it’s too long and because I don’t understand it!

Twin Primes are adjacent odd numbers both of whom are prime. It is known that these twins occur more often than would occur randomly but what, if any significance twin primes have is unknown. But they’re just cool! (Credit: Twitter)

Mathematician love to find new properties of primes that they can study and calculate, and the latest news is about a certain kind of prime that has been christened a ‘digitally delicate prime’. Simply put, digitally delicate primes are multi-digited prime numbers that if you change any one of their digits to any other number the resulting number is no longer prime.

Take the number 294,001, which it turns out is the smallest of all digitally delicate primes. This number is prime but if you change any of it’s six digits to any other number, change the 4 to a 6 for example, and the number you get, 296,001, is no longer prime. Now 294,001 has 6 digits, any one of which can be changed to any of 9 other numbers, the 2 say could be changed to 0 or 1 or 3, 4, 5, 6, 7, 8 or 9! That’s 6×9=54 other numbers, none of which are prime, so you can see that just checking to be certain if a prime is digitally delicate or not can be a lot of work.

Delicate primes were first introduced back in 1978 by mathematicians Murray Klamkin and Paul Erdős.  Erdős in fact not only found a few examples of digitally delicate primes but also proved once again that there are an infinite number of digitally delicate primes.

Why doesn’t the Math Olympics get the media coverage the athletic ones do? Murray Klamkin is well known for the problems he developed for the math games. (Credit: Ebay)

The latest development comes from a mathematician at the University of South Carolina named Michael Filaseta who has described a new class that he calls ‘widely digitally delicate primes’. To get a widely digitally delicate prime you take a digitally delicate prime and add a bunch of zeros out front, taking 294,001 and making it 000,000,294001 for example. Remember from high school if you add a zero in front of a number you don’t really change the number, 09 is still just 9 and 000,000,294,001 is still just 294,001.

Doctor Filaseta wearing the first dozen or so digitally delicate primes. He can’t wear any widely digitally delicate primes because, despite having proven they exist he hasn’t found one yet! (Credit: Quanta Magazine)

But what if you change one of those zeros out front to another number, is 000,000,294,001 still a digitally delicate prime like 294,001 is? No, in fact 010,294,001 is not a prime number so 294,001 may be digitally delicate but it is not widely digitally delicate. Doctor Filaseta has actually not yet succeeded in finding a widely digitally delicate prime, but get this, he has managed to nevertheless prove that one exists somewhere.

If you were thinking right now, what practical applications does any of this arithmetic have, why would anyone bother doing all these calculations? Well for centuries people thought the same thing about prime numbers in general. It’s only in the age of high-speed computers and computer hackers that very large prime numbers have found a use as a means of securing sensitive Internet communications.

On the whole I agree with Sir Arthur. But, as I know he’d agree, physicists wouldn’t be able to get very far without all those mathematical tools the idol worshipers have generated. (Credit: Today in Science History)

But more importantly studying number theory in general advances our knowledge of mathematics and in a very real sense our ability to understand the Universe in which we live depends on our understanding of mathematics. That’s why math is often called the ‘Queen of the Sciences’.