We all remember square roots from our high school math classes. You know, since 3 times 3, formally 32 squared, equals 9 that means that the square root of 9 is 3. Some numbers, like 9 have nice round square roots like 3. Other numbers, have square roots that are irrational, that is the number never comes to an end and never repeats itself. The square root of 17 is 4.12310563… for example.

Negative numbers are a special problem because you’ll remember that a negative number times another negative number gives a positive number. Therefore -3 times -3 is +9, not -9. So what is the square root of -9? Does it even have one?
(By the way, if you’ve always had difficulty imagining why a negative times a negative gives a positive consider this metaphor. Someone films a bathtub while water is draining out of it. That film is then shown running backwards! The water draining out is a negative, running the film backwards is also negative but what you would see is the water rising in the tub. A positive!)
For along time mathematicians simply ignored the possibility of the square root of a negative number. Such things just don’t exist they said. Then a sixteenth century Italian mathematician named Cardan was trying to find two numbers that when added together equal 10 but when multiplied equal 40. The solution he got was:
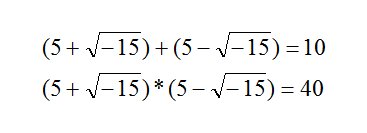
Cardan himself wrote that his solution was meaningless, fictitious and imaginary. But it worked. It worked so well that mathematicians quickly figured out how to contain the madness as it were.
What they did was to define an imaginary number, i2=-1, not i= √-1, the number i is actually never defined, only its square is. Nevertheless anytime mathematicians came across a √-1 they would replace it with i. So for example √-16=√16*√-1=4*√-1=4i.
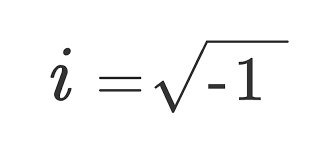
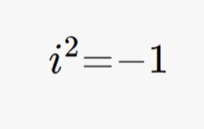
Formally the square root of a negative number is called imaginary, like 4i, but a combination of an imaginary number and a real number is called a complex number, 5+4i would be an example where 5 is the real portion and 4 the imaginary part. All complex numbers have a strange counterpart called the complex conjugate where every i has its sign changed, i→-i and -i→i everywhere. Whenever a complex number is multiplied by its complex conjugate the result is always entirely real, for example taking the most basic complex number A+iB where A and B are both real numbers and i2= -1 the complex conjugate would be A-iB and:
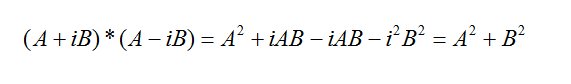
The terms in i cancel each other out while the i2 term =-1. Since A and B are both real A2+B2 is totally real. For a time it was thought, or perhaps hoped would be a better word, that imaginary and complex numbers were just mathematical fictions, with no application in the real world. However it was found that the familiar trigonometric functions could be expressed as complex functions.
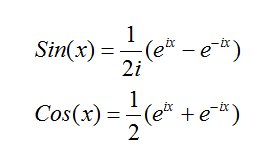
Physicists meanwhile were starting to use the sin and cos functions to represent waves of varying kinds, light waves, sound waves, alternating current in electrical systems etc. Things got even worse during the development of quantum mechanics when the wave nature of subatomic particles became evident and the solutions ψ(x,t) of the Schrödinger wave equation:
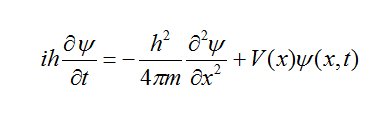
are always complex. It was physicist Max Born who figured a way out of this dilemma when he suggested that ψ itself is not observable, its only when ψ is multiplied by its complex conjugate ψ* giving ψψ*= real that the answer to the Schrödinger equation becomes an observable. Schrödinger himself considered the presence of all those i’s in his equation to be unpleasant writing to a fellow physicist that “ψ is surely a fundamentally real function.” This is where physics has remained now for nearly a century with the solutions to our equations giving complex answers but we only pay attention to the so-called ‘real’ part.
Now a group of theoreticians has proposed a thought experiment wherein the reality of imaginary numbers is required and it involves another of quantum mechanics strange properties, quantum entanglement. The basic idea of quantum entanglement is that if you measure the state of two particles those particles are now entangled and even if you separate them the measurement of them as a system must remain the same.
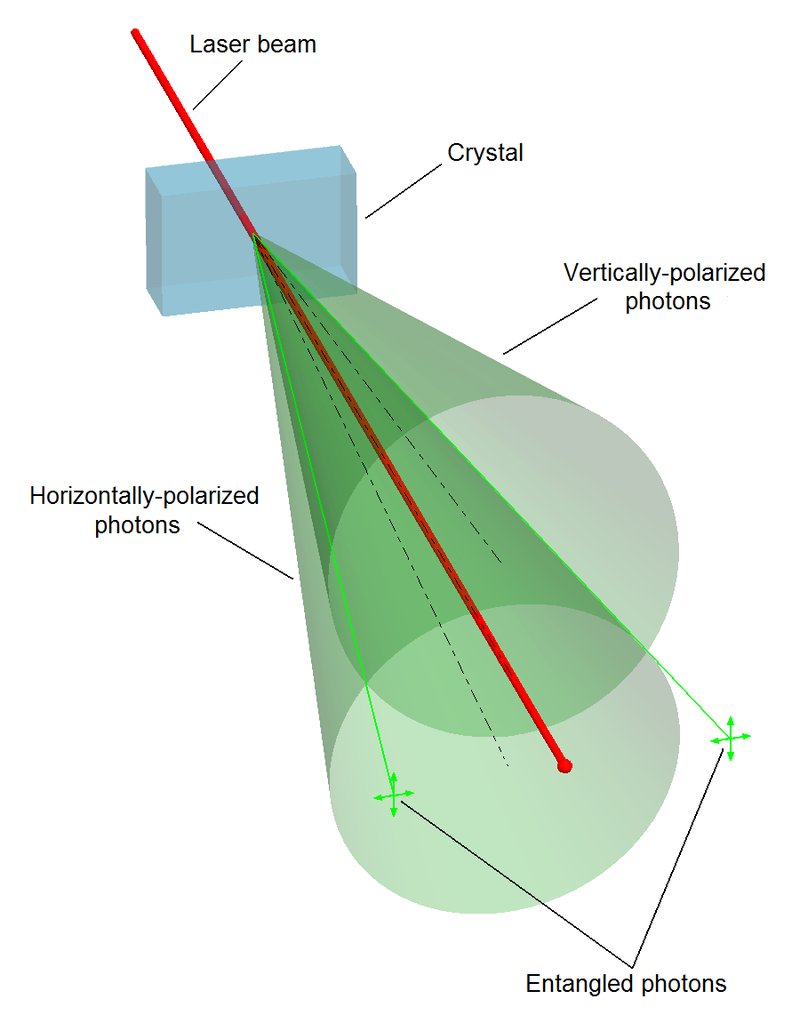
To put it more simply, if you measured a system of two coins and found it to have one head and one tail and then separated them by a great distance. Once separated if you measure one to be a head, then the other must be a tail no matter how far apart they now are. (Mind you the trick is to separate the two particles or coins without breaking the entanglement.) This effect has been both demonstrated and calculated using only the real parts of the wave function ψ.
The new thought experiment starts by making things more complicated. Let’s say I have two entangled particles and send one to a friend in California named Perry and the other to a friend in Florida named Nancy. Another physicist in Illinois also has a pair of entangled particles and sends one to Nancy in Florida and the other to a friend in Massachusetts named Bill. Notice how the second set of particles doesn’t come from me.
Now the question. Are the two particles received by Perry and Bill entangled, keeping in mind that Nancy got one from each of us? Well the only way to get the answer that everyone expects to be correct, remember this experiment hasn’t been performed yet, is by assuming that the imaginary part of the wave function of the entire system has a physical reality.
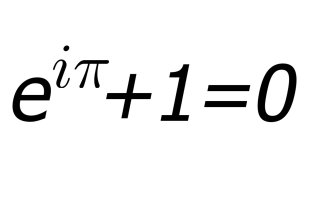
At the moment the paper, which includes physicists Marc-Olivier Renou of the Institute of Photonic Sciences in Spain and Nicolas Gisin at the University of Geneva, is undergoing peer review so these results are preliminary. Also, if the groups thought experiment does survive scrutiny you can bet someone is going to try to perform the experiment for real.

Imaginary numbers have befuddled both mathematicians and scientists for going on 500 years now and will undoubtedly continue to do so for even longer. The whole thing seems so simple, yet so weird, and trust me if you don’t pay attention you can screw them up so easily. I guess maybe it’s just a little more evidence of how important our imagination is in understanding reality.
