Every field of scientific research has its own ‘highest honour’ the award that is given to those researchers who have made the greatest contribution in that field. For Physics, Chemistry and Physiology that award is of course the Nobel Prize but for Mathematics the highest honour is the Fields Medal, which are awarded just once every four years by the International Mathematics Union. The Fields Medals also differ from the Nobel in another way because they are given, not to older mathematicians for a lifetime of achievement but to mathematicians under the age of forty who are currently doing important and impressive work.

This year the Union announced on July 5th that they had chosen four young mathematicians for the award. The winners are Maryna Viazovska of the Swiss Federal Institute of Technology in Lausanne, aged 37, Hugo Duminil-Copin, 36 of the Institut des Hautes Études Scientifiques near Paris France, James Maynard, aged 35 of the University of Oxford in England and June Huh of Princeton University in New Jersey, USA, aged 39.

Maryna Viazovska is only the second woman ever to receive the Fields Medal and she did so for her pioneering work in the stacking of equal sized spheres in dimensions higher than three. This problem of how to most efficiently stack spheres, sometimes also known as stacking cannonballs, was first considered by the great mathematician and physicist Johannes Kepler. After considerable study Kepler decided, but couldn’t rigorously prove that the way soldiers stacked their cannonballs was the most efficient but the problem remained unsolved until mathematician Thomas Hales at the University of Michigan succeeded in 1998 with a 250 page proof.

In the years since Kepler mathematicians have become interested in spaces with more dimension than the normal, like the four dimensions of Einstein’s space-time. As you might guess problems like stacking spheres become more difficult with each added dimension. Back in 2016 Doctor Viazovska succeeded in finding the best solution in eight dimensions, calling her arrangement E8. Then, only a week later and with the help of four other mathematicians she used E8 to find the solution in 24 dimensions.

Was it just luck that the solution in 8 dimensions allowed her to quickly find the solution in 24 dimensions? Doctor Viazovska doesn’t think so, she’s certain that there’s a connection and if she can find out what that connection is it may lead to more solutions in other dimensions.
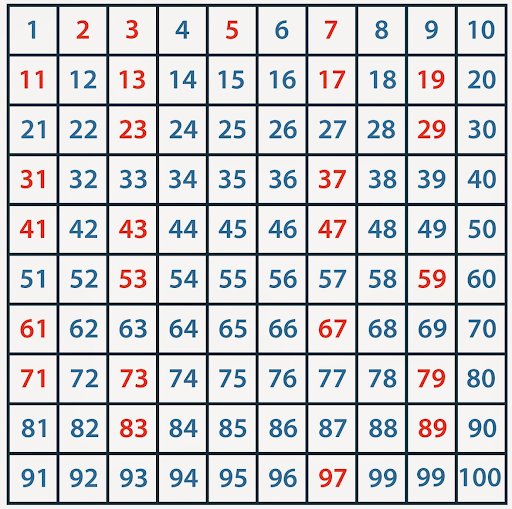
Meanwhile at Oxford University James Maynard is one of many mathematicians over the years who have fallen in love with prime numbers, those numbers like 7, 11 or 29 that can only be evenly divided by themselves or 1. Doctor Maynard’s work concerns the famous twin prime conjecture. That’s where, once you find a prime number, let’ say 11, the number just two later 13 is also very often another prime. This pairing has been known for centuries and as far as we know, goes on forever. (Remember since all even numbers can be divided by two, that makes two itself the only even prime, all other primes are odd.)

As the numbers get bigger the density of primes gets smaller, for example there are 24 prime numbers between 0 and 99 but only 14 between 900 and 999. Despite the growing space between them in 2013 a mathematician named Yitang Zhang at the University of New Hampshire was able to prove that there was an infinite number of prime pairs and that the separation between them was always less than 70 million.
Extending Doctor Zhang’s work what Doctor Maynard has succeeded in doing is to reduce that separation to less than 600. Additionally Doctor Maynard was able to show that there are an infinite number of primes that do not end in a 7. One more little piece in the puzzle of the most interesting group of numbers there is.
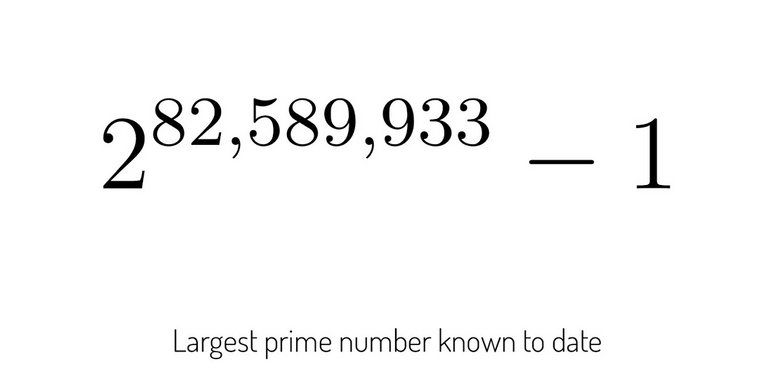
On the other hand Doctor Hugo Duminil-Copin is a little more practical, in fact during college he had difficulty in deciding whether to be a mathematician or a physicist. Doctor Duminil-Copin’s research deals with the mathematics of what are known as phase transitions, a very complex subject indeed. Phase transitions are sudden, large-scale changes in the characteristics of a material, such as when liquid water freezes into ice.

Phase transitions are also important in the magnetic properties of materials. Consider an ordinary bar magnet made of iron for example. The reason why a bar magnet is a magnet is because each of the atoms of iron in the bar is itself a tiny magnet, and if enough of those atoms are aligned in the same direction then the entire bar will become a magnet.
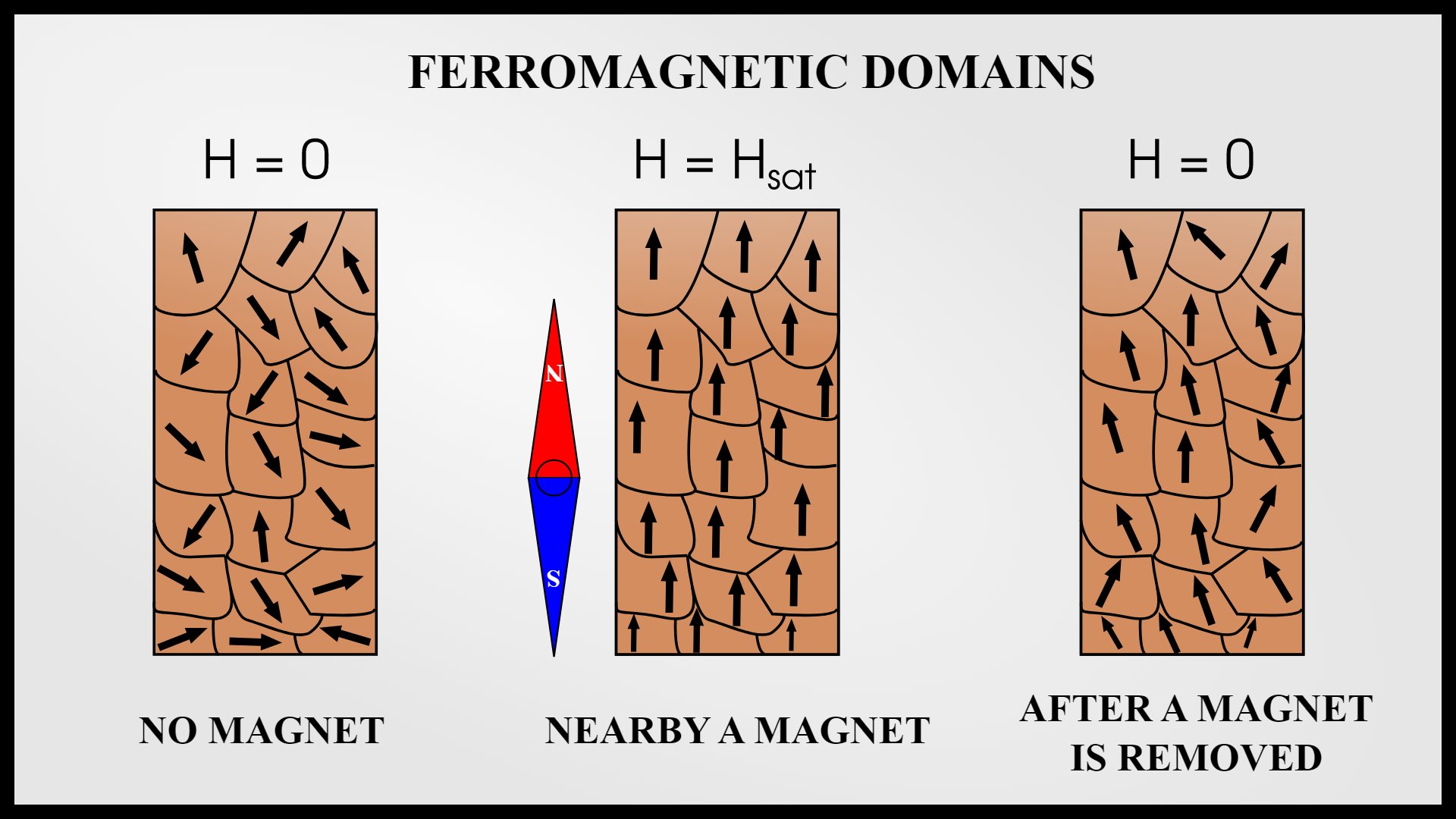
However, if that bar magnet is heated, then at a certain temperature, known as the Curie temperature, the atoms will start to alter their orientation, they will start to point in random directions once again and the bar will lose all of its magnetic properties. Also, if a bar of iron at a temperature above the Curie temperature is placed in an external magnetic field the atoms will line up and then, if the bar is cooled back below the Curie point, the atoms will freeze in place and the bar will then become a permanent magnet.
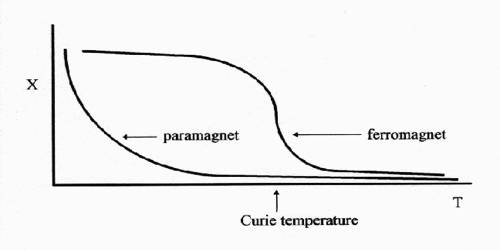
The standard model for this phase transition from non-magnet to magnetic, and vice versa, is known as the Ising model after German physicist Ernst Ising who solved the one dimensional version of the problem in 1924. The two dimensional version of Ising’s model wasn’t solved until 1944 and the three dimensional version, obviously the one physicists are most interested in, has never been exactly solved. To date only approximate solutions, often generated by computers, are available, but these approximations leave several very important questions unanswered.
What Doctor Duminil-Copin has done is to connect the problem of magnetic phase transitions to the better understood process of percolation of a liquid through a porous material. By doing so Doctor Duminil-Copin was able to show that some of the characteristics of the two dimensional Ising model are still true in three dimensions, in particular that while the phase transition may be rapid, it is still a continuous process, not a discontinuous jump like water into ice.
Finally when June Huh was growing up in California and South Korea he never expected to become a mathematician, in fact he wanted to become a poet. When his writings failed to get published however he decided to major in physics and astronomy at Seoul National University, hoping to become a science writer. In his senior year of college however he met a previous winner of the Field’s Medal, Doctor Heisuke Hironaka who was teaching a course in algebraic geometry. It was that course that turned Doctor Huh into a mathematician.

Doctor Huh’s field of research is known as combinatorial analysis, basically studying the different ways that a number of objects can be put together to form a single system. One well known method of calculating these combinations replaces each object in the system with a colour and considers the colour combinations using a set of functions called chromatic polynomials. By calculating these polynomials mathematicians gain insight into the possible combinations of a set of objects and Doctor Huh has found success in his calculations by using some of the tools he learned in algebraic geometry from Doctor Hironaka.
So that’s a brief glimpse at the work of this year’s Field’s Medal winners in Mathematics. Each recipient in their own way is extending of boundaries of mathematics and just simply giving us a better understanding of the way things work.
