Did you ever take a rubber or foam ball or other object and squeeze it or pull it, changing its shape. If you did then you performed an operation from a branch of mathematics called Topology, the study of geometric shapes and spaces. That said, much of the work of topologists concerns the relationship between two shapes or the ways that one shape can be morphed into another.

Consider the shape of a baseball and an American football, obviously they are pretty closely related. Pull on the opposite sides of the baseball and you’ll get the shape of a football while if you push in the ends of the football you can make it round like a baseball. If you think about it that’s also true of a frankfurter, it’s just a sphere that’s really been stretched. Stretching, squeezing, twisting and bending are one set of operations that can be performed to change the shape of an object. Two shapes are considered to be homeomorphic if the can be transformed one to the other by only stretching, squeezing, twisting or bending.
Now consider the baseball and a doughnut. It’s pretty obvious that you can’t go from one to the other just by Stretching, squeezing, twisting or bending, it’s that hole in the doughnut that makes it a completely different kind of object. In order to make, or eliminate the hole you have to perform an operation like cutting, tearing or gluing. So topology recognizes two distinct classes of operations. On the other hand a doughnut and a coffee mug are considered to be homeomorphic because you can squeeze and massage a doughnut shape into that of the mug, even forming the bowl of the mug, without either cutting tearing or gluing.

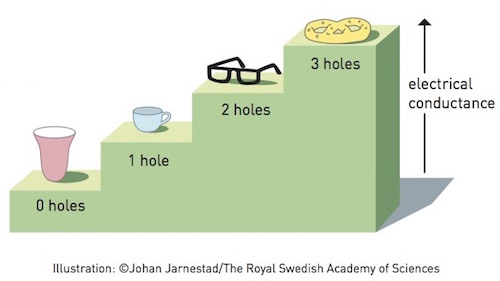
We can also perform the same sort of exercise with the letters of the alphabet in capitals to discover that they fall into a series of classes:
No holes with a continuous, but not necessarily straight line:
(C, G, I, J, L, M, N, S, U, V, W and Z)
No holes and three tails: (E, F, T and Y)
No holes and four tails: (H, K, and X)
One hole and no tails: (D and O)
One hole and one tail: (P and Q)
One hole and two tails: (A and R)
Two holes and no tail: (B)
It is simple to see how any member of one class can be transformed into another member of the same class by shaping, but not a member of another class.
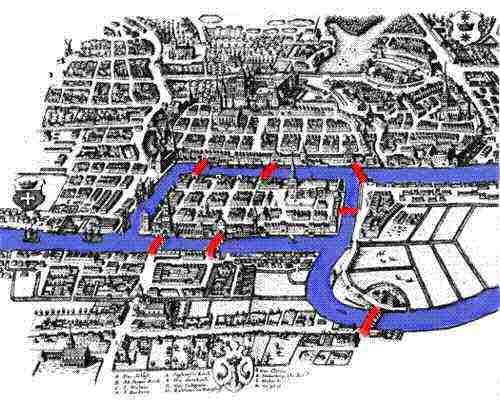
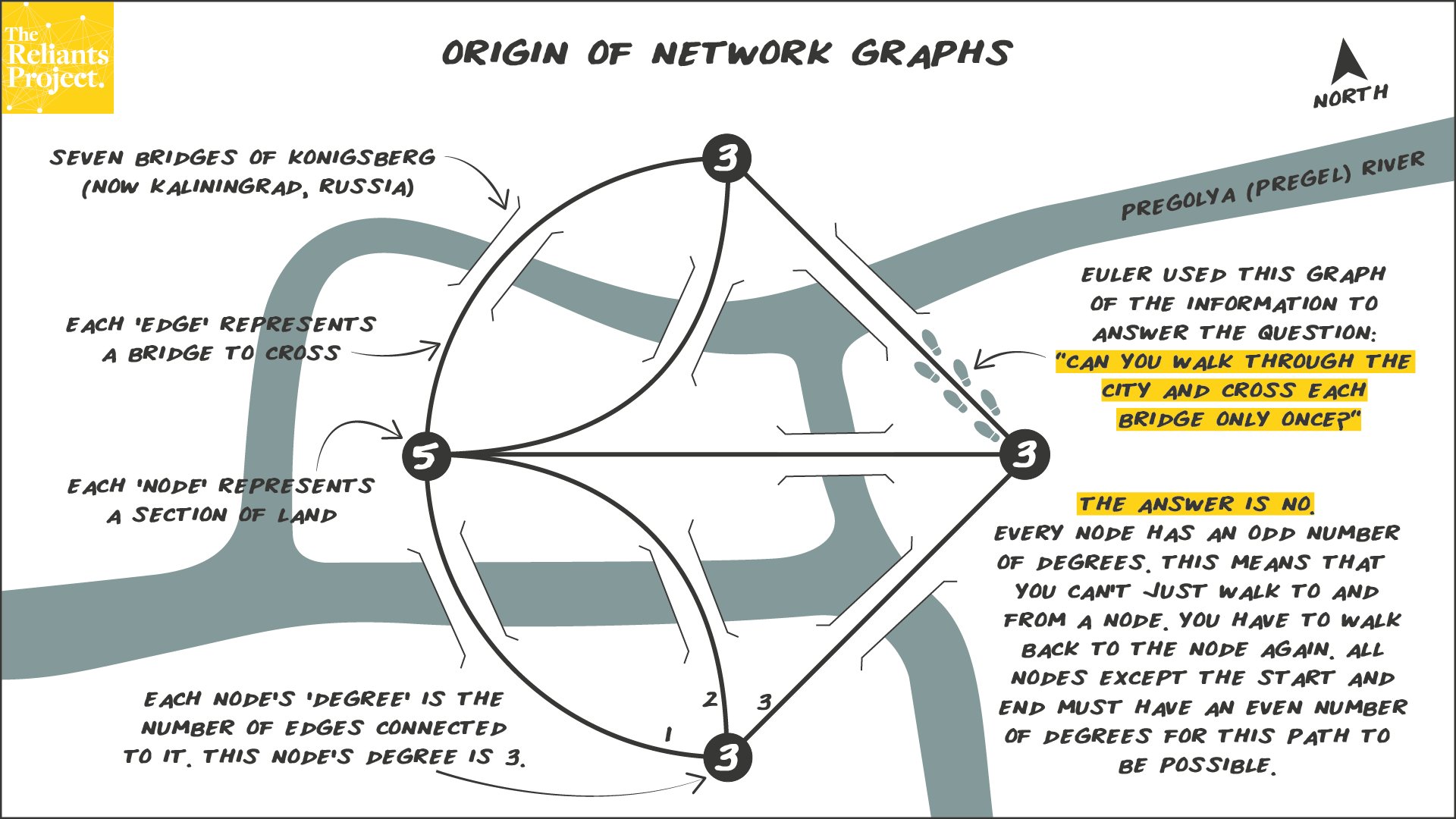
Historically Topology is considered to have started with a famous problem stated by the mathematician Leonhard Euler in 1736 known as the ‘Seven Bridges of Königsberg’. In this problem, see figure below, the question is can someone cross all of the seven bridges of the town of Königsberg, modern Kaliningrad, without crossing any bridge twice. The answer is no but obviously the analysis is a study of shape and connections.
Other similar problems were studied over the years after Euler. One interesting one is known as the ‘hairy ball’ theorem, which states that it is impossible to comb the hair on a hairy ball without creating a cowlick somewhere. Again the ball can really be any smooth 3D shape, so long as it contains no hole. And in case you think that mathematicians are just playing silly games with a ‘hairy ball’ the more formal name for the theorem, that a continuous tangential vector field on such a surface must be non-vanishing, is of considerable importance in many types of field research.

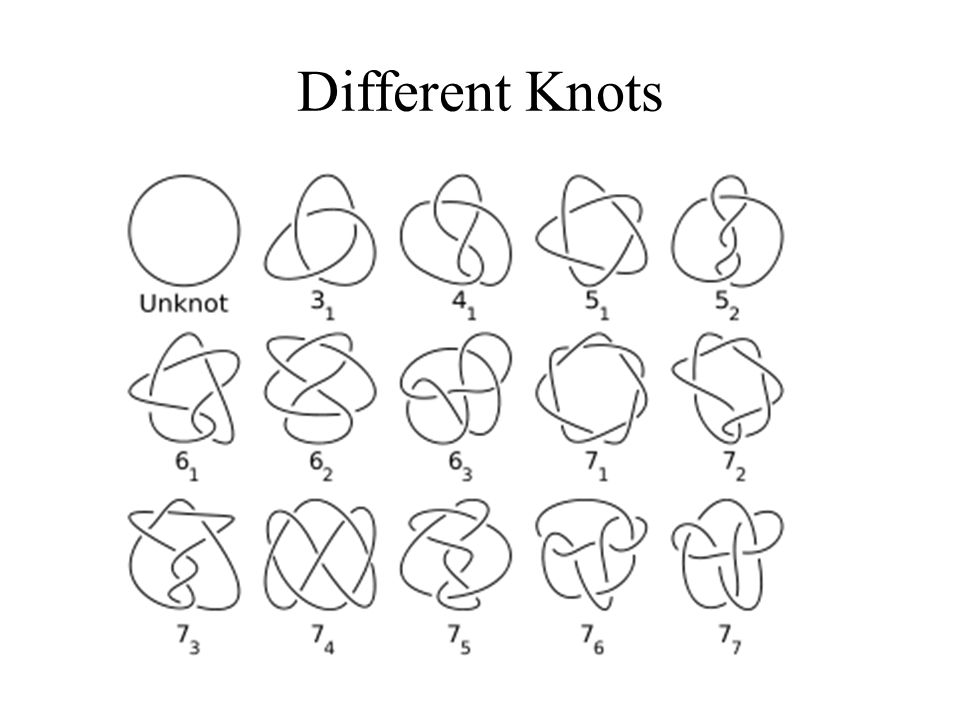
It wasn’t until the year 1847 that Johann Benedict Listing first used the term ‘Topologie’ in an article entitled ‘Vorstudien zur Topologie’. Since that time different topology has seen several distinct sub-subjects develop including algebraic and differential topologies along with the original geometric topology. Other fun sub-subjects of topology are knot theory and set topology.
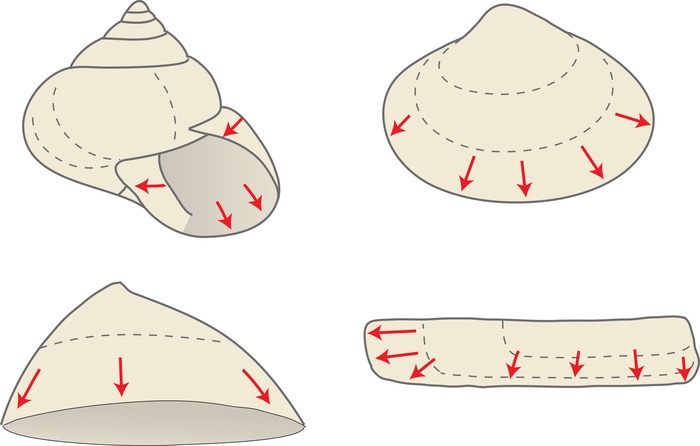
In modern science topology is becoming an ever more important mathematical tool. In evolutionary biology the morphing of a clamshell into a snail shell is studied by topology revealing the genetic pathways that generated the two classes of molluscs. In biochemistry the shapes of proteins and nucleic acids are analyzed by knot theory.
In physics topology has been used in condensed matter physics along with quantum field theory and perhaps most important of all in cosmology, by studying possible shapes and structures for the Universe as a whole. While some aspects of topology, like the seven bridges problem are both easy to understand and fun to analyze, topology is also a very subtle mathematical discipline, which can take years of study to master. A proposal well worth the effort.
