We’re all familiar with the way that certain geometric figures, the square being the simplest, can be fitted together so there are no gaps or overlaps, the pieces all fit together perfectly. This geometric property is known as tiling because throughout history we humans have tiled floors and walls both for construction and to produce works of art.

As I said there are some geometric figures that can be tiled like squares, rectangles, triangles, and hexagons. At the same time there are geometric shapes that will not produce a perfectly fitted tile, like stars, five or six sided, and octagons. There are also tiled patters that can be formed using two different geometric figures like a diamond and a parallelogram (see figure below). In mathematical terms such figures or combinations of figures are said to ‘admit’ tiling.
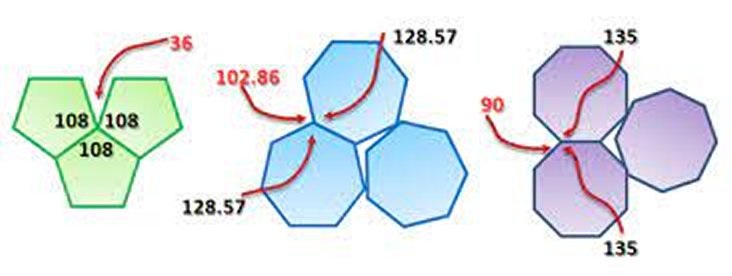
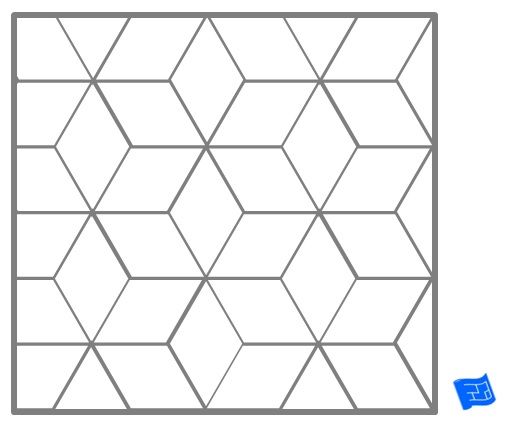
You may have noticed that all of the figures I mentioned above are straight lined shapes rather than curved figures like a circle or a teardrop. While it is true that it is easier to find straight lined shapes that tile there are many known curved shapes that tile as well.

Mathematicians have explored the properties of tiled patterns ever since the days of the ancient Greeks, if not even earlier. One of the most important features of the tiling of geometric figures is that they almost always repeat themselves over and over again in identical patterns. For some of the more elaborate geometric shapes, and especially for combinations of two or more figures the repeating section may be quite large, nevertheless the greater majority of tiled figures repeat themselves over and over again.

Those few combinations that do not repeat themselves have been given the special name of Penrose tiles after a small class of which was discovered back in the 1970s. Since then mathematicians have searched in vain for an elusive ‘Einstein’ tile, a single geometric figure that would tile perfectly but without creating a repeating pattern. (By the way the name Einstein does not refer to physicist Albert Einstein but rather to the meaning of the German word einstein, ‘one stone’.

Now a group of mathematicians from a quartet of Universities, Yorkshire, Cambridge, Waterloo and Arkansas, have found that elusive one stone, a thirteen sided irregular figure that they have christened ‘the hat’. As can be seen in the figure ‘the hat’ obviously does not develop a simple repeating pattern. In order to officially declare their result to be an einstein however the researchers had to prove that there would never be a repeating pattern by using what is known as a geometric incommensurability argument.

The mathematicians who discovered ‘the hat’ expect that the most likely use of their figure will be in the arts and I’m certain it won’t take long before some artist takes up the challenge. Which brought to my mind what artistic creations the celebrated graphic artist Maurits Cornelis Escher, better known as M. C. Escher, might have done with ‘the hat’. Escher became famous both for turning tiled geometric figures into living animals, but also by then using those ‘living tiles’ in a larger work of art that contained less abstract elements as well.
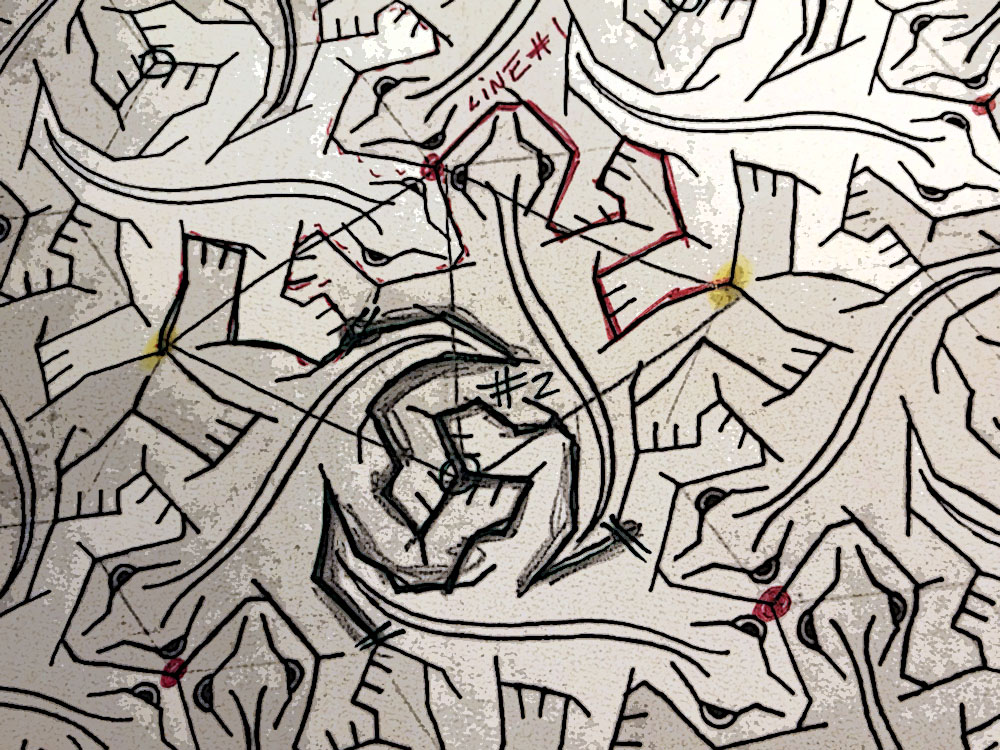

M.C. Escher lived from 1898 to 1972 in the Netherlands producing woodcuts, lithographs and mezzotints rather than paintings or sculptures like most of his contemporaries. Most of Escher’s works were greatly inspired by mathematical ideas, including artistic explorations of infinity, reflection and even hyperbolic geometry. During much of his life Escher was mostly ignored by the arts community, even today many artists regard him more as an uninspired workman rather than a true artist. In scientific circles however, Escher’s ideas and inventiveness slowly gained him a large following, one that continues to grow to this day.


Escher produced literally dozens of ‘living tiles’ using birds, fishes and even human beings as the tiled shape. Arguably the most famous of his tiled efforts is ‘Reptiles’, see figure above, which contains a page with a tiled pattern of lizards but at one end live lizards are coming out of the page, walking around a bit before sinking back into the flat reptile pattern.

Throughout his work Escher was fascinated by repeated patterns of one, two or even three geometric figures, many of which he would turn into living creatures. I’m certain that Escher would have been thrilled by the challenge of working with ‘the hat’, a figure that tiles but never repeats.
