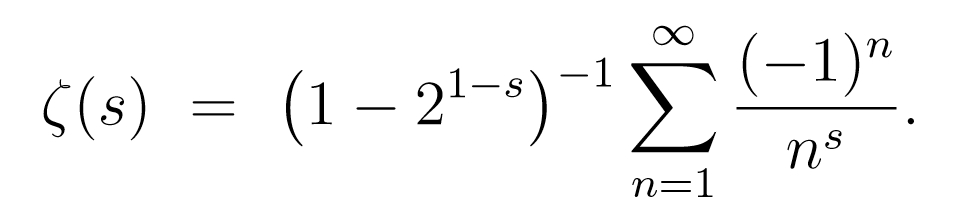Tag: Mathematics

One of the Oldest Problems in Mathematics is yielding new results.     

It may be the oldest problem in mathematics; it’s a problem we deal with on a regular basis. How do we divide up a single object, let’s say a pie or cake, so that everyone gets a piece and there’s nothing left to go to waste. Remember some people, like my brother and I like big pieces while some people, like my sister want a smaller piece. In the end all of the various fractions that we cut that cake into have to add up to one, that one cake.

However you do it. When you cut cake the two most important requirements are that everyone gets a piece and nothing goes to waste. Surely that’s one of the oldest problems in mathematics. (Credit: Association for Computing Machinery)

Put in mathematical terms the problem consists of finding a set of integers, let’s say the set (2, 3, and 6) the sum of whose reciprocals 1/2+1/3+1/6=1! We know from archaeological evidence that this problem has been considered since the time of the ancient Egyptians but it had to have been around much longer. After all even Neanderthals had to carve up that deer they killed into pieces that added up to one.

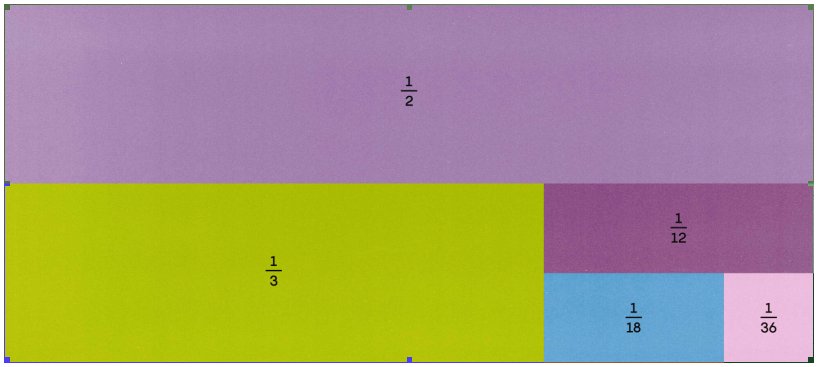
Carving up a rectangle into five different sized pieces, with each piece being the reciprocal of a natural number, an interesting mathematical game. (Credit: Quanta Magazine)
Ancient Egyptian papyrus discussing how to cut up an object into different slices. So it is a problem mathematicians have worked on for a long time. (Credit: Quanta Magazine)

Now of course it’s easy to cut up our cake into n number of pieces each of which is 1/nth of the whole, 8 pieces that are each 1/8th of the pie, pizza chefs get a lot of experience at doing that. Mathematicians however like to make things more complicated so they want to consider solutions where each piece is a different size, and just to make things really interesting they prefer to only use fraction whose numerator is 1 like 1/2 or 1/8 or 1/124, such fractions are technically known as unit fractions because of the number 1 in their numerator. Using unit fractions mathematicians can then search for patterns in the numbers of the denominators, like my example of 2, 3 and 6 above. In this way they can learn about the hidden structure in the numbers that we use everyday.

Unit fractions, with the number one in the numerator and a positive integer in the denominator, may seem simple but they contain a great deal of hidden structure. (Credit: The School Run)

Back in the 1970s this ancient problem got a new twist as the mathematicians Paul Erdős and Ronald Graham published a conjecture that stated that any set of numbers that was sufficiently large, a condition known as positive density, must have a subset of numbers whose reciprocals add up to 1.

As famous in some circles as any rock star or pro athlete, Paul Erdos sure loved his numbers. (Credit: Twitter)

Problem was that few mathematicians, including Erdős and Graham, had any good idea about how to prove their conjecture. So the whole idea kind of just sat there for almost fifty years before a mathematician named Thomas Bloom of Oxford University in England was given an assignment to do a presentation on an effort to prove the Erdős-Graham conjecture by Ernie Croot 20 years ago using the colouring method. In this method numbers are sorted into different baskets by a designated colour. Using a branch of mathematics known as harmonic analysis Croot was able to show that no matter how many baskets were used, at least one would contain a set of numbers fulfilling the Erdős-Graham conjecture. Croot used a type of integral called an exponential sum, which can calculate how many integral solutions there are to a problem. The problem is that exponential sums are almost always impossible to solve exactly so Croot’s methodology was unable to answer the full, positive density version of the conjecture as originally stated by Erdős and Graham.

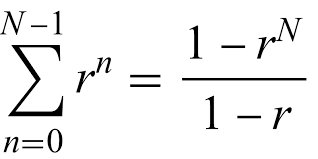
One of the simpler exponential sum formula, many can only be approximately solved using modern computers. (Credit: Wolfram MathWorld)

But reading Croot’s attempt did get Thomas Bloom thinking about the Erdős-Graham conjecture and he brought his own expertise in combinatorial and analytic number theory to the problem. Bloom’s technique allowed him to have greater control over the approximation of the exponential sum so that in the end he succeeded in proving not that there was a solution but that the number of solutions was positive and an integer, meaning there had to be one or more solutions.

Thomas Bloom of Oxford University is the latest, but certainly not the last, mathematician to contribute to the problem of ‘How should we slice a cake?’. (Credit: Quanta Magazine)

Just another example of how mathematicians can reexamine even the oldest of problems and still find new structure, new patterns. Showing once again that mathematics is the queen of the sciences. 

Using a Slime Mold as an inspiration Mathematicians in Japan have developed a simple solution to the Traveling Salesman Problem.

Right now the entire world is working its way through one of the most difficult logistical problems it has ever faced. The Pfizer Covid-19 vaccine, which has some very stringent storage requirements, has to be distributed as quickly as possible, well everywhere on the planet! It’s not an easy problem to solve, trying to find the most efficient way of getting the vaccine to literally every human being, and remember the longer it takes to get the vaccine to everyone the more people will die!

The First shipments of the Pfizer Covid-19 vaccine was carried live on several news channels! When has the simple act of shipping a product ever received such media attention! (Credit: Marketwatch)

Obviously shipping directly from the factory to each individual would not be the optimal solution, even if the vaccine didn’t have to be stored at a temperature of -70ºC. So instead you designate a number of depots, hospitals in the case of a vaccine, that receive shipments from the factory and then the depots distribute the vaccine to individuals.

The distribution of the Covid-19 vaccine is an enormous and complex problem and remember, lives are dependent on getting it right the first time! (Credit: StirlingUltracold)

In that case how many depots? Where should they be? What about a multi-layered approach where the factory ships to major depots that ship to smaller, more local depots in turn who then distribute the vaccine to individuals? So, how many layers? It’s a lot of questions to answer, and remember, people are getting sick every minute!

Real life situations like the Covid vaccine are members of a class of mathematical problems known as the ‘Traveling Salesman Problem’ or TSP. In its most simple description a salesman is required to visit N number of cities and wants to calculate the shortest possible route connecting them all. Remember the longer the journey the more time it takes and time is money after all. TSP is considered to be one of the classic problems in mathematical optimization.

The Traveling Salesman Problem is a mathematical problem in combinatorial optimization. (Credit: Slideshare)

For two cities the solution is pretty obvious. Travel to one city, then straight to the other and then back home, which city you visit first doesn’t matter since going along exactly the same path in the reverse order still leads to the same total distance. As you add cities however the problem quickly becomes much more complicated. Consider three cities, which we shall name 1, 2, and 3. There are in fact six separate combinations that get you to all three cities as shown in Table 1.

The six different paths you can use to visit three cities. In terms of distance however the combinations in the top row are equal to the combination directly beneath them so there are really only three solutions. (Credit: R. A. Lawler)

However once again following the same path in exactly the opposite direction leads to the same total distance traveled so there are really only three solutions, see Table 2. Each of these distinct solutions now has to be evaluated to determine which is the shortest.

The three unique solutions for three cities. (Credit: R. A. Lawler)

Adding one more city to bring the number to four increases the number of different combinations to 24, see Table 3. And even after we after we reduce the number by half to account for symmetry that still leaves us with 12 distinct paths to be evaluated for total distance, see Table 4.

Adding only one more city greatly increases the number of different paths. This is typical of combinatorial problems in mathematics. (Credit: R. A. Lawler)
For four cities there are 12 distinct paths. (Credit: R. A. Lawler)

So if our traveling salesman wants to visit two cities there is only one path for him to follow, for three cities there are three distinct routes, for four cities 12. As more cities are added the numbers just explode, five cities yields 60 routes and before long you’ve reached the point where even a supercomputer will have to take a good bit of time to find the optimal, shortest path. In fact the TSP is so simple yet so enormous a problem that it is often used to evaluate the performance of new computer and software designs and methodologies.

The Traveling Salesman Problem is both enormous yet simple. Because of these factors it is often used to evaluate the performance of the world’s best computers. (Credit: CNET.com)

Now in real life it usually isn’t necessary to find the absolutely best route. Think about it, if there are 50 million possible solutions then there are probably at least a thousand that are within 0.1% of the optimal. If one of that thousand can be found quickly it may make more sense to get started with a good solution rather than wait for a supercomputer to find the perfect one.

This is certainly a good route but is it the best one? Maybe a good route quickly is better than the best route later! (Credit: Algorithm Repository)

That’s why mathematicians at Hokkaido University in Japan have developed an analog computer that quickly finds a good solution to the TSP by mimicking the feeding behavior of, Slime Mold! You see slime molds are large, single celled organisms that are capable of deforming their bodies in a manner similar to an amoeba. In their search for food a slime mold will send out a number of tendrils is several directions. Those tendrils can sense the chemical traces of nutrients so tendrils that sense food nearby get bigger and longer and form sub tendrils while those that don’t sense food shrink.

Slime Molds are single celled organisms that are experts at finding the nutrients they need and ignoring everything else. (Credit: Quanta Magazine)

In this way a slime mold will very quickly find any available food and shape its body to take advantage of any resource. Inspired by the slime mold’s search methodology Professor Seiya Kasai and his student Ph.D. candidate Kenta Saito designed an analog circuit where resistance values are used to represent distances. A breadboard circuit for a four city problem was built that quickly found a solution that, if not the best, was significantly better than the average solution.

Block Diagram for an circuit that would solve the eight city problem. (Credit: ResearchGate)

The circuit is so designed that additional cities can be easily added and the amount of time required to find a good solution only increases linearly with the number of cities added. In other words while it would take a digital computer five times longer to calculate the best five city solution than the best four city solution, it only takes the analog circuit 25% longer to find a good five city solution.

The slime mold solution to the problem of designing the railroad network for the greater Tokyo area! Not bad! (Credit: ptc. Parking Consultancy and Traffic Engineering)

In the real world a good solution now is often better than the best solution later, remember time is money and in many cases lives. Slime molds took millions of years to evolve a practical way to solve the traveling salesman problem, now we can profit from their instinctive knowledge. Another example of science learning by studying nature.

Sum of three cubes problem finally solved for the number 42, the last of the natural numbers to be solved.

Mathematicians like to solve problems, that’s what doing math is after all, solving problems. In fact mathematicians enjoy problem solving so much that they often make some up just in order to have the fun of solving them.

Of course Mathematicians also enjoy a good joke! (Credit: SketchUp Community)

One such problem is the sum of three cubes for the integers between 0 and 100. This problem was initially posed in 1954 at Oxford University and is sometimes known as solutions for the Diophantine equation.

The problem, simply stated is, can a solution be found for the equation:

x3+y3+z3=k                                                 (equation 1)

Where k is an integer between 0 and 100 and x, y, and z are integers not necessarily between 0 and 100 nor even positive.

One example is easy to construct:

13+23+33=1+8+27=36                                 (equation 2)

Using that solution, and remembering that x, y or z can be negative quickly gives three more solutions.

(-1)3+23+33= -1+8+27=34                      (equation 3)

13+(-2)3+33=1-8+27=20                                   (equation 4)

(-1)3+(-2)3+33=-1-8+27=18                          (equation 5)

I’ll give one more playful solution:

23+33+43=8+27+64=99                                (equation 6)

Again using negative integers quickly allows three other solutions to be constructed but I’ll leave them for the student to discover as they say.

You can play at individual solutions for a while but if you try to work methodically starting at zero you quickly run into problems. For example zero itself only possesses the trivial solution:

(a)3+(-a)3+(0)2=0                                        (equation 7)

Where a is any integer. If any non-trivial solution existed for zero it would in fact be a counterexample to Fermat’s famous last theorem.

For k=1 or 2 there are in fact families of solutions. For k=1:

(9b4)3+(3b-9b4)3+(1-9b3)3=1                            (equation 8)

Where b can be any integer. The family of solutions for k=2 is:

(1+6b3)3+(1-6b3)3+(-6b2)3=2                            (equation 9)

Again b can be any integer. To check these solutions it’s instructive give them a try for a nice small number like b=2 and see how they work out!

By the way you are allowed to use the same integer more than once as in this solution for k=3:

13+13+13=3                                                 (equation 10)

O’k, so we’ve found some of the easy solutions but finding solutions for most integers quickly becomes very difficult. So difficult in fact that many solutions only became possible with the aid of electronic computer. Even with the assistance of the world’s best computers solutions for some integers proved elusive.

Indeed, after 65 years two numbers remained for which there was no known solution, 33 and 42. Then earlier this year the University of Bristol mathematician Andrew Booker managed to grab a couple of weeks time on the university’s supercomputer. The solution he obtained for 33 is:

Professor Andrew Booker of Bristol University found the solution to 33 and collaborated on the final solution, 42. (Credit: Phys.org)

88661289752875283+(-8778405442862239)3+(-2736111468807040)3 =33                                                                       (Equation 11)

So now the only number left without a solution was 42. Fans of the British Radio/TV/Book series ‘A Hitchhikers Guide to the Galaxy’ by Douglas Adams may recognize 42 as the answer to the ultimate question about ‘Life, the Universe and Everything!’ Now the fact that the final number lacking a solution should be a fan favourite is of course just a coincidence. Nevertheless a solution for 42 proved to be an order of magnitude more difficult to obtain.

The Hitchhiker’s Guide to the Galaxy began as a radio program on the BBC, was made in Television, then a series of books and finally a movie. (Credit: Amazon)

Realizing he needed even more computing power Booker teamed up with MIT professor Andrew Sutherland, an expert in parallel computing. This is a technique where numerous computers work simultaneously on different parts of the same problem. Professor Sutherland set up a massive ‘planetary computing platform’ consisting of the spare, unused time of half a million home PCs.

Another Andrew, Professor Andrew Sutherland of MIT who organized the computer system that succeeded in cracking the solution to 42. (Credit: MIT Math)

It took one million hours of computing time, which is still only 2 hours per computer after all, but the solution to 42 was finally found.

(-80538738812075974)3 +804357581458175153+ 126021232973356313 =42                                 (Equation12)

So all of the numbers k between 0 and 100 have now been solved, but there’s no reason to stop at 100 is there? The smallest number now without a solution is 114 so get out a pencil and paper and get busy!

Mathematician Sir Michael Atiyah claims that he has proven the Riemann hypothesis concerning the distribution of Prime Numbers.

Sir Michael Atiyah is considered to be one of the World’s leading mathematicians; he has already received two of the highest awards in the field, the Fields Medal and the Abel Prize. And the Riemann hypothesis, that an equation known as the Riemann zeta function can produce all of the Prime Numbers, has been called math’s most important unsolved problem. So when a top mathematician announces that he has solved the biggest problem its major news. The image below is Sir Michael.

Sir Michael Atiyah (Credit: Scientific American)

But that’s just what happened on the 24th of September on a stage at the Heidelberg Laureate Forum. At that forum Sir Michael presented what he himself described as a “radically new approach.” Dr. Atiyah’s proof will still have to be reviewed by other mathematicians before it will be accepted but the very possibility of that this problem could be solved has riveted the math world.

Now I don’t pretend to completely understand Sir Michael’s proof, yet. I just downloaded a copy and am working my way through it, remember I’m a physicist not a mathematician specializing in number theory. However I hope that I can explain something about prime numbers and why the Riemann hypothesis is so important.

We’ve all heard of prime numbers, those numbers that are divisible only by the number one 1 themselves. For example, while the number 6 can be written as 2×3, the number 7 can only be written as 1×7, 7 is a prime number. The prime numbers below 100 are given below. (one is traditionally not considered prime).

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.

Now take notice first of all that the number 2 is the only even prime number. That’s because all of the other even numbers can be divided by 2. You can also see how the distance between successive prime numbers is getting bigger, primes spread out as the numbers get bigger.

We’re not certain whether it was the Egyptians or Mesopotamians who first noticed that primes were different from other numbers but we do know that it was the Greeks, either Pythagoras or one of his students, who proved that there were an infinite number of primes. The proof is simple, and only takes three lines so what do you say. Shall we give it a try?

We will start by assuming that there is only a finite number of primes, let’s say p1, p2, p3, through  pn, that is we have n prime numbers total. Now we will demonstrate that that assumption is false. First we multiply all n of the prime numbers and add 1 to get, I’ll call it X.

X= (p1 x p2 x p3 x  …x pn) +1

Now, if we divide X by any of the primes, let’s say pi there will always be a remainder of the 1/pi. This means that either X must itself be prime, or evenly divided by some other prime not in our set of primes. In either case our assumption that we had all of the primes must be wrong, there are an infinite number of prime numbers.

O’k so how do we find those numbers that are prime? Is there some equation that will generate all of the primes for us?

Well, mathematicians searched for just such an equation for a very long time. Several partial equations, that is formulas that worked for a while, generating some primes were developed. One of the greatest mathematicians of all time, Bernhard Riemann worked for many years on prime number theory, his equation is known as the Riemann Zeta function. By the way Bernhard Riemann also developed the equations of geometry that Einstein used for his theory of gravity. The image below is Bernhard Riemann and beneath him is his Zeta function.

Bernhard Riemann (Credit: Famous Mathematicians)

The Riemann Zeta Function (credit: Public Domain)

Riemann published his zeta function back in 1859 and in the years since then it has been checked, and confirmed, for the first 10,000,000,000,000 (that’s ten trillion!) primes but that doesn’t mean that it will work for all primes. Remember there are an infinite number of primes so ten trillion is actually not very many!

Sir Michael Atiyah claims to have proven that the zeta function works for all primes and if he’s right that will be a tremendous achievement. Other mathematicians now get to try to pull the proof apart. We’ll see what happens.