Anyone who is familiar with physics today knows that the mysteries being studied are pretty esoteric in nature. Things like Black Holes, Dark Energy, Marjorana Particles, Quantum Gravity; these are the subjects that occupy the physics community nowadays. The behaviors of everyday objects in our everyday world, those problems were all solved by Galileo and Newton, weren’t they?

Well, not quite. Turns out there are still a few problems; usually dealing with a large number of objects under special circumstances that physicists have never really been able to solve rigourously. Today I’d like to discuss two of these problems, one of which has finally been solved and another whose solution remains elusive.
The first problem, the one that has recently been solved is a familiar one to anyone who has shopped for fruits or vegetables. Greengrocers wanting to display their tomatoes or apples or other nice round fruit commonly do so by spreading them out on an inclined plane, see image below:

Now, if you look closely at the peaches, plums, apples and oranges in the image you’ll see that by stacking them in tightly the fruits all form a nice hexagonal array. The question is, when a customer takes a single fruit out of the display what are the chances of them causing a collapse or avalanche of the entire array. Or to put it another way, how many fruits can be taken out of such an array before a collapse occurs.
Seems simple enough doesn’t it, but remember there are a lot of different particles, different individual fruits that is, and each and every fruit exerts a force on every other fruit. That’s right even the mass of the orange on the upper right exerts a force on the orange at the bottom left and, keeping in mind Newton’s third law that “For every action there is an equal and opposite reaction” that means that the orange at the bottom left exerts a force on the orange at the top right. Oh, and let’s not forget that the angle at which the oranges are stacked is certainly going to be a factor.
So you see the whole mess gets really complicated really quickly which is why physicists have hated problems like this throughout the 18th, 19th and even the 20th century. That’s why the solution had to wait until the 21st century and the development of supercomputers. That’s right the physicists who solved the problem did so but running a vast number of numerical simulations, they let the computer do the arithmetic.

The physicists, Eduardo Rojas, Hector Alarcon, Vincente Salinas, Gustavo Castillo and Pablo Gutierrez all hail from three universities in Chile, the Universidad de Autofagasta, Universidad Autonoma de Chile and the Universidad de O’Higgins. For their simulations they considered identical spherical balls each with a diameter of 4cm and a mass of 2.93 gm, basically tennis balls. Altogether the team ran simulations with 90 balls with 6 rows alternating between 7 and 8 balls each. They then scaled up that basic array to arrays of 372, 846, 1512 and 2370 balls.

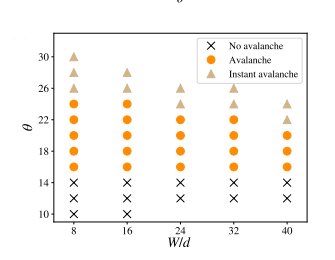
The first thing the physicists found was that for very low angles an avalanche may never occur, obviously if the angle is zero you could lift out every ball with no collapse occurring. Conversely for a very high angle removing even a single ball can cause an avalanche. The interesting results came, as I’m sure you guessed, from medium angles. After numerous simulations were run the researchers found that avalanches typically occurred after 10% of the balls were removed and that the original number of balls in the array had only a small effect on that percentage.
So the next time you’re in the local supermarket and you reach for that one perfect apple in a big display, rest assured that you probably won’t cause all of the apples to go tumbling onto the floor. Unless of course several other customers have already plucked out their apples.

The other everyday physics problem is one that will also have a familiar feel about it. Imagine a large container that is only partially filled with a variety of mixed nuts, some small like peanuts or almonds, some large like walnuts and hazelnuts. Now you want to have all of your nuts nicely distributed so that anyone who wants a peanut just has to reach in and take one off the top while anyone who wants a hazelnut can do the same. So you put a lid on your container and give it a good shake for a minute or so to get all the nuts scrambled together.

Problem is that when you open the container what you find is that the top layer is completely made up of the big walnuts and hazelnuts with all of the smaller nuts down at the bottom. And it’s not the shape of the objects that causes the effect, you can do the same experiment with BBs and marbles, the smaller BBs will go to the bottom while the larger marbles end up on top.

On the one hand it doesn’t make sense, you’d think that the larger, heavier objects would be able to force their way to the bottom. But at the same time maybe the small sized objects are able to squeeze their way between the bigger objects so that they end up on the bottom.

The plain fact is that the smaller objects do go to the bottom but we really don’t know how. Again the problem seems simple enough in detail but when you consider dozens or even hundreds of objects the amount of arithmetic quickly becomes a nightmare. Like with the fruit avalanche problem above the ‘Hazelnut Problem’ as it’s often call, or more formally Granular Convection, will hopefully one day be solved by thousands of simulations carried out on a supercomputer.

There you have it, two ‘classic’ problems in physics that neither involve field theory, nor particles traveling near the speed of light or getting too close to a black hole. Two ordinary problems in everyday life. One of which took hundreds of years to solve while the other remains unsolved.
