It may be the oldest problem in mathematics; it’s a problem we deal with on a regular basis. How do we divide up a single object, let’s say a pie or cake, so that everyone gets a piece and there’s nothing left to go to waste. Remember some people, like my brother and I like big pieces while some people, like my sister want a smaller piece. In the end all of the various fractions that we cut that cake into have to add up to one, that one cake.

Put in mathematical terms the problem consists of finding a set of integers, let’s say the set (2, 3, and 6) the sum of whose reciprocals 1/2+1/3+1/6=1! We know from archaeological evidence that this problem has been considered since the time of the ancient Egyptians but it had to have been around much longer. After all even Neanderthals had to carve up that deer they killed into pieces that added up to one.
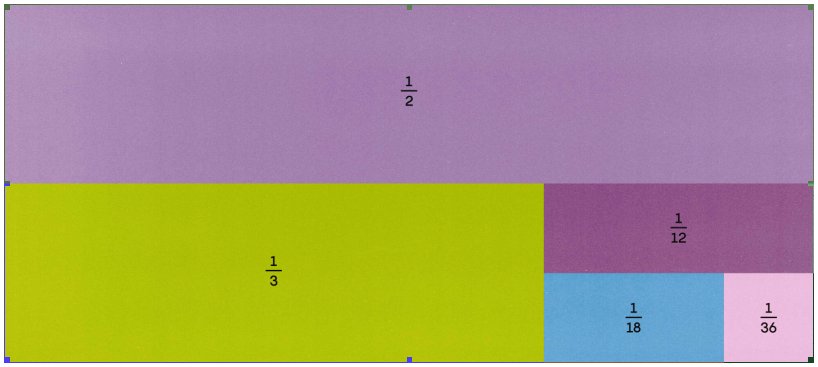

Now of course it’s easy to cut up our cake into n number of pieces each of which is 1/nth of the whole, 8 pieces that are each 1/8th of the pie, pizza chefs get a lot of experience at doing that. Mathematicians however like to make things more complicated so they want to consider solutions where each piece is a different size, and just to make things really interesting they prefer to only use fraction whose numerator is 1 like 1/2 or 1/8 or 1/124, such fractions are technically known as unit fractions because of the number 1 in their numerator. Using unit fractions mathematicians can then search for patterns in the numbers of the denominators, like my example of 2, 3 and 6 above. In this way they can learn about the hidden structure in the numbers that we use everyday.
Back in the 1970s this ancient problem got a new twist as the mathematicians Paul Erdős and Ronald Graham published a conjecture that stated that any set of numbers that was sufficiently large, a condition known as positive density, must have a subset of numbers whose reciprocals add up to 1.

Problem was that few mathematicians, including Erdős and Graham, had any good idea about how to prove their conjecture. So the whole idea kind of just sat there for almost fifty years before a mathematician named Thomas Bloom of Oxford University in England was given an assignment to do a presentation on an effort to prove the Erdős-Graham conjecture by Ernie Croot 20 years ago using the colouring method. In this method numbers are sorted into different baskets by a designated colour. Using a branch of mathematics known as harmonic analysis Croot was able to show that no matter how many baskets were used, at least one would contain a set of numbers fulfilling the Erdős-Graham conjecture. Croot used a type of integral called an exponential sum, which can calculate how many integral solutions there are to a problem. The problem is that exponential sums are almost always impossible to solve exactly so Croot’s methodology was unable to answer the full, positive density version of the conjecture as originally stated by Erdős and Graham.
But reading Croot’s attempt did get Thomas Bloom thinking about the Erdős-Graham conjecture and he brought his own expertise in combinatorial and analytic number theory to the problem. Bloom’s technique allowed him to have greater control over the approximation of the exponential sum so that in the end he succeeded in proving not that there was a solution but that the number of solutions was positive and an integer, meaning there had to be one or more solutions.

Just another example of how mathematicians can reexamine even the oldest of problems and still find new structure, new patterns. Showing once again that mathematics is the queen of the sciences.
